データ分析の解析アプローチについてざっくり説明したところで、次は記述的統計解析による実際のデータ解析の流れを説明していきます。
数の情報を表現するのは、数字で描くよりグラフで表すのが最も効果的です。また分析するときにもまず入手したデータを、複雑な統計解析を行う前にまず図や表の形にして分析することで
データが持つ情報についての思わぬ見落としを防ぐことができたりします。特にグラフなどの視覚情報は数字の羅列よりもわかりやすく、直感的な理解を可能となります。
そして棒グラフは、空間的ないし時間的に分布する数量の比較に有用です。横軸に時間をとる時系列データの場合は線グラフを使うことが多いです。
また、比率や%で表される値は円グラフで示すと、全体がどのように構成されているのかが一目でわかりので便利です。また他にも、度数分布図(ヒストグラム)というものもあります。
これは、データの大きさによってクラス分けし、クラスごとの頻度を視覚化するものです。並べ替えた数字よりは見やすいですが、近い値の数字が集まるところは 点が重なってしまいわかりにくいという欠点があります。
そういう時は、そこでデータの値を、例えば階級分けし、その階級に分類されるデータの数を階級ごとに示す度数分布表を使います。
こんなやつ↓


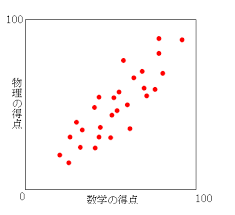
そして2変数の関係を分析したいときは、まず散布図を描きましょう。これにより、関係が線形なのか、非線形なのか、異常値が無いかなどを確認することができます。
この他にも数多くのグラフがあり、これらはエクセルなどを使って簡単に作成することが可能です。
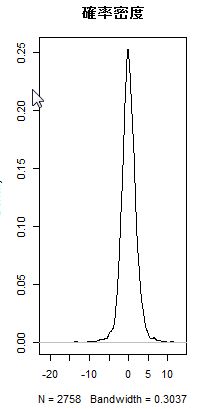
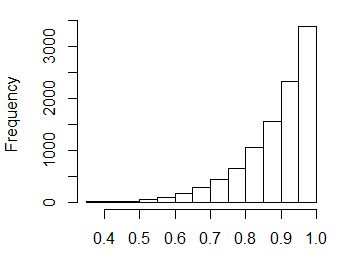
また、度数分布図(ヒストグラム)を描くことで、データの分布についての様々な特徴を捉えることができます。下の図は いろいろ分布の例を R で描いたものです。
分布の中心的傾向とは、発生頻度の高い集団が分布上のどこに位置するかという特徴です。分布の広がり(ばらつき)の度合とは、分布が中心近辺に固まっているのか、広い範囲にばらけているのかという特徴です。
分布の歪みとは、左右対称な分布に比べて形状が歪んでいるかどうかということです。頂上が右よりになっているとき、左裾が長くなるので左への歪みと言います。
分布の裾の厚さとは、中心から離れた事象の発生確率がすぐに小さくなる場合裾が薄い、なかなか小さくならない場合に裾が厚いと言います。このように、ヒストグラムを描くことで分布の特徴を捉えることが可能となります。


また平均や中央値や分散といったデータの代表値は、これらの分布の特徴を1つの数値で表現するものであり、多くのデータを比較分析する際に便利な手法であり、データの基本的手法となります。
Q:データ分析ってまず何をすればいいんですか?
A:まずExcelやRでデータをグラフ化して、平均や分散といった基本統計量を求める。
追記:データ分析については、統計学に頼らないデータ分析「超」入門 という本が、読んでいて分かりやすかったのでオススメです。
