統計学における分析手法は、2つの要素を線形で表す単回帰分析や複数の要素を分析する、クラスター分析などの多変量解析などはエクセルでも簡単に行うことができ、
世間一般でも比較的有名ですが、時系列分析はエクセルで行うのは少々面倒なため、他の解析手法に比べて、あまり浸透していないような気がします。
統計学の基本は回帰分析なのですが、統計学の最先端は分野は、研究成果がそのまま「カネ」に繋がる金融市場で、
そこではどういう分析手法が一番大事なのかというと、株式や為替といった金融商品の価格変動の時系列データというわけです。
回帰分析だと、なにかの要因から結果を予測しますが、時系列解析では、過去のデータから未来を予測するという分析になります。
まず時系列データにおける基本統計量を紹介していきます。
回帰分析では平均、中央値、最頻値、分散・標準偏差が基本統計量でしたが、時系列分析では、分散(ボラティリティ)・期待値・自己共分散・自己相関係数が基本統計量とされています。
前回も述べたように、時系列モデルは確率構造で考えることが一般的なので単なる平均ではなく、期待値が基本統計量とされています。期待値とは、確率変数Xの実現値を確率の加味して平均した値のことです。
ギャンブルにおける期待値は、掛け金に対して戻ってくる見込みの金額をあらわしたものです。(パチンコや宝くじが負けるといわれている理由は期待値の金額が出費よりも少ないからです。株やマージャンは確率の要素が複数あるので人によりけりです。)
簡単な計算例としては、10%の確率で10000円、40%の確率で1000円、50%の確率で0円がもらえる宝くじがあったとすると、期待値は10000×0.1+1000×0.4+0×0.5=1400円となります。
分散は、各時点でのデータが期待値からどの程度までばらつく可能性があるかというものを表す統計量です。分散が大きいほど値のばらつきが大きいことを意味しています。
分散の値の目安は特になく、平均と比べたり作図して考慮します。そして、分散の平方根√をとったものを標準偏差といいます。(もし、分散が4ならば標準偏差は√4=2ということになります。)
分散と標準偏差については下の記事でもっと詳しく説明しています。
分散はファイナンス分野では、ボラティリティと呼ばれています。ボラティリティは、暴落レシオなど金融市場において、リスクを計測するための指標として用いられています。
まあここまでは高校でならったり、回帰分析で出てくるところなので問題ないでしょう。そして、ここから時系列分析独特の統計量の説明に入っていきます。こいつらが時系列分析においてもっとも大切なところです。
自己共分散と自己相関係数は時系列データの系列相関を表現する基本的統計量です。
※共分散がXとYという別々な2つなデータの関係性を表したものであるのに対して、自己共分散は、同一の時系列データにおける、2つの異なる時点の共分散を指します。同じデータで共分散を計算するので、前に自己とつけているだけで共分散と同じです。
※共分散については↓を参照
例えば、時系列{Y1・・・・Yn}における、ある時点Ynと、そこからk時点ずらしたYn-k についての自己共分散cov(Yn,Yn-k)は以下のように求められます。
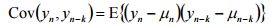
※μnは時系列{Y1・・・・Yn}の期待値です。
自己共分散は、時点を一定の幅でずらした場合のそれぞれのデータに対して、相関があるかどうかを示す統計量となります。
自己共分散とは、完全な相関を示したときを σの2乗 として、そのラグにおいて時間シフトしたデータとそのデータの実現値がどれだけ似ているかを、示す尺度と考えることができる。
ちなみにk時点離れた時系列の自己共分散のことを、k次の自己共分散といいます。また、自己共分散をkについての関数で表したものを自己共分散関数といいます。
全体的にデータが右肩上がり(正比例)の分布になっている時には自己共分散が+に、右肩下がり(反比例)の分布になっている時には自己共分散が-になります。
そして、共分散が、大きくなると両者はより連動して変化するようになり、小さくなると無関係に近い関係ということになります。
ですが、ここで1つ問題が出てきます。(自己)共分散の数値は元のデータの単位やデータの量に依存しているために、場合によっては非常に大きな計算結果になります。
たとえば体重と身長の相関関係と、体重とカロリー摂取量の相関関係は、どちらの方がより強い関係性があるのか?という問いがあったとしたら、サンプル数や単位が異なる場合には比較ができません。
この問題を解決するのが自己相関係数です。
(自己)共分散は上で述べたように、対象データの単位に依存して値が変化するという点があります。というわけで、自己共分散の値をもっと分かりやすくするため、自己共分散を分散(σの2乗)で正規化します。
これを自己相関係数といいます。自己相関係数の範囲は −1~1 に収められます。
自己相関係数(ACF)の求め方は下のようになります。
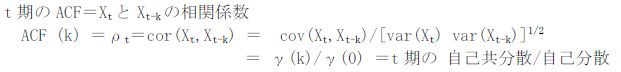
※var()は分散を意味しています。
ちなみに(自己)相関係数の目安は下のようになります。
0 ~ 0.2 :相関はない
0.2 ~ 0.4 :弱い相関がある
0.4 ~ 0.7 :相関がある
0.7以上 :強い相関関係がある
自己相関係数の絶対値が1に近いときは、時刻の値はひとつ手前の値により、かなりの精度で予測できるということになります。
共分散と相関係数は計算がめんどうですが、別に計算できなくても計算はコンピューターが勝手にしてくれるので意味が分かれば問題ないです。
原系列のデータをもとに以上の統計量を推定することは、変動幅や将来の値の予測を行うという時系列データ分析の目的に大きく関連します。
しかし、期待値や自己相関は一般的に時点tに依存するにもかかわらず、時系列データは一度しか観測できないという問題があります。
つまり、予測を考える場合でも、将来の観測値が存在しないため、自己相関などの統計量を評価することはできません。
そこで、その確率変数列(時系列データ)の生成過程に関して何らかの性質や構造を仮定してそれに合っているかというアプローチを行っていきます。
そして、このような確率変数列の確率構造を仮定したものを時系列モデルといいます。時系列分析の概念と基本統計量について説明したところで、次は代表的な時系列モデルの簡単な紹介をしていきます。
追記:時系列分析についてはこちらの本がとても分かりやすかったです。時系列分析がよくわからないという方にとてもオススメです。
